我现在来想挑战一下对振动的了解。有人说,是共振创造了世界。对振动过程所遵循的规律是什么、什么是共振、共振又遵循什么规律、在振动过程中还有哪些新鲜的事物我还没有接触并了解的……这些我很兴趣的内容。
简谐振动
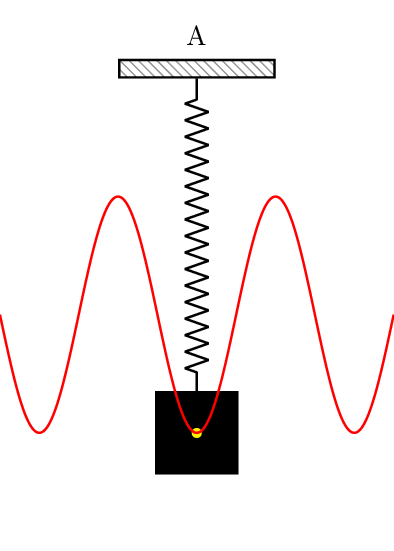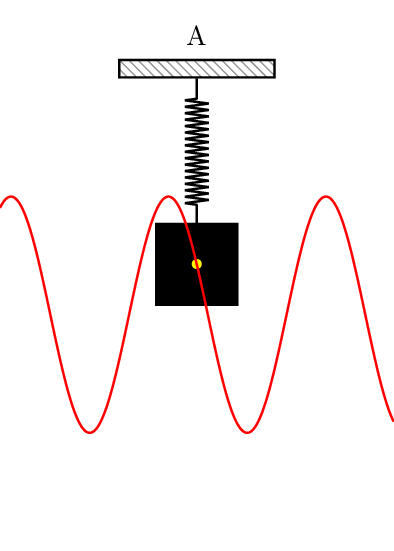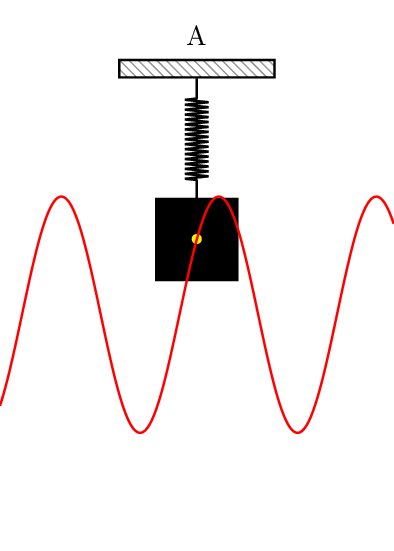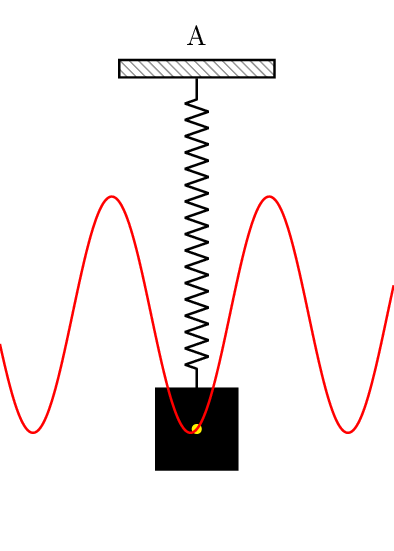
最理想最简单的振动是简谐振动。
什么是简谐振动?
简谐振动是指正中央是平衡点的正弦或余弦振动,且振幅和频率是常数,无阻尼振动。
简谐振子:把振动物体看成不考虑体积的质点(或点电荷),也叫谐振子、振动质子。
简谐振动无驱动无摩擦,振幅与相位由初速度决定。
所以,简谐振动是一种理想的振动。理想情况的分析最容易发现某个概念的“本质”特征,去除“非本质”特征。
简谐运动方程的解
简谐振动方程由牛顿第二定律和胡克定律建立起来的。
由牛顿第二定律公式,可得式1:

由胡克定律,可得式2:
![]()
由上面两式合并,可得式3,这个式子就是简谐振动方程:

这个方程的解是什么(即x等于什么)?
我们根据两次微商之后还可以得到x,我们可以断定x是正弦函数或余弦函数,所以简谐振动方程的解为式4:

考虑到振子的初始状态有振幅,且有初始相位,上式可得如下式5:
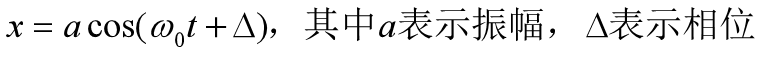
由于cos(ω0t +Δ)可以展开,可得式6:
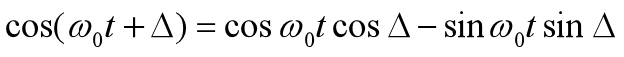
所以,式5展开之后 可写成的形式如式6:

为了简化和方便,我们将式6写成的形式如式7:
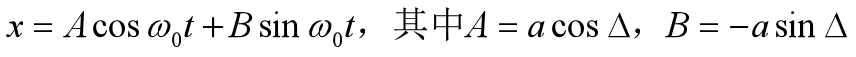
(编者评:看来,从任意相位出发的振动,都可以看成两种从最小振幅和最大振幅开始的振动的合并)
如果我们求振子的速度,则式7求微商,可得式8
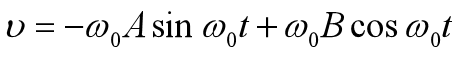
所以,当振动开始时(即t=0),并将t=0代入式7和式8中,可得式9和式10
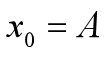
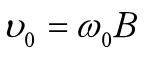
从式9和式10可知,x0和v0是指初始时的离开平衡位置的位移和初始时的速度,一旦知道初始条件,我们就可以求出A和B。
如果需要的话,我们又能从A和B的值求出a和Δ。
所以,只要知道初速度和振幅,我们就可以得出简谐振动方程的解。
简谐振动的能量守恒
由于没有摩擦和外力,能量就应该守恒
我先由式5推导出速度公式,可得式11

现在,我们来推导一下振动过程中的动能和势能。
动能用T表示,弹性势能用U表示,则可得如下两式,分别是式12和式13
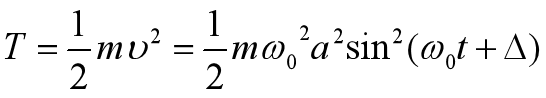
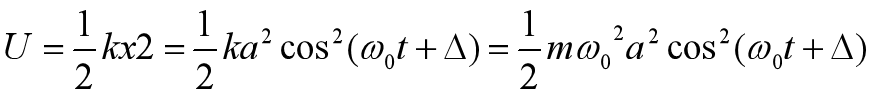
当我们将T+U时,
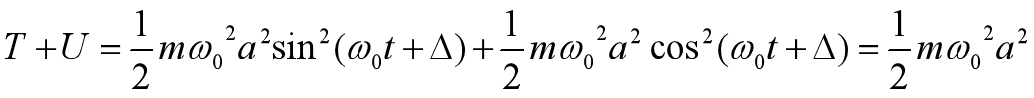
我们发现可得到一个常数,这说明简谐振动是一个能量守恒的过程,而且能量与振幅的平方成正比。式子如上,式14
也就是说,如果振幅增大为原来的两倍,那么振动的能量就是原来的四倍。
(编者评:上面的推导没有一处随意产生的,简谐振动的能量是守恒的,与振子质量、振幅的平方、物质的固有角频率的平方成正比。既然这个公式成立。虽然简谐振动是一种理想情况,但简谐振动的能量与振幅的平方成正比却是一个无比可靠的结论,一切形式的简谐振动也应该成立。所以,这一结论,对于电荷振动也是成立的。)
受迫振动
受迫振动是指振动受到一个外策力(外策力可以与时间有各种函数关系)。此时还不考虑振动中受到的摩擦力。
受迫振动的方程如式15

假设,外策力随时间发生周期性变化的,也称为力是振动的。则力F可以写成式16
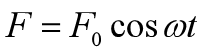
所以式15可以写成式17
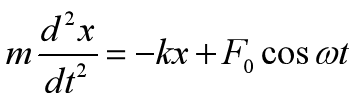
根据这么一条规律,受迫振动的频率与驱动力的频率相同,与固有频率无关。我们完全可以猜想上述方程有这么一个解,即式18
![]()
其中C是一个待确定的常数,ω是外驱力的驱动频率,也是受迫振动的频率。将式18代入式17中,得到式19

其中ω0指的是固有频率。将式19进一步变形,我们就可以求出C的值,如式20
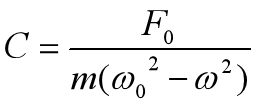
由上式我们知道了常数C的值。从式18,我们知道C值其实代表了振幅。
共振
进一步分析可知,当ω远小于ω0,意味外力影响有限。或者ω远大于ω0,此时振动的振幅也不会很大。
在上述ω远小于或远大于ω0时,外策力也是瞬间响应的,则外策力的影响更是微乎其微。
值得注意的是,当ω和ω0非常接近,C将趋向无穷大。即力与固有频率“合拍”,振幅将会很大,比如荡秋千,如果推力周期或频率与秋千频率相同时,推力将会增大振幅,如果是乱推,秋千就荡不起来。
但事实是,振幅不可以有无穷大,这是因为我们还没有将摩擦力及其他力考虑进去。振幅虽然不会无穷大,但ω和ω0非常接近时,却可能使得弹簧断裂!
我们把ω和ω0非常接近时,引起振幅变大的情况称为共振。
有阻尼的受迫振动
很多情况下,摩擦力与物体的运动速度成正比。比如一个物体在油(或很浓的液体)中作低速运动时摩擦就是如此。所以,我可以将摩擦写成式21
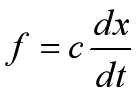
所以,振动方程变成了式22
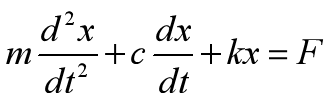
为了数学分析方便一些,我们可以将常数c写成c=mγ,则上式可变成式23
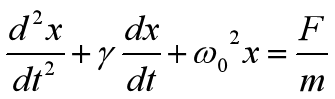
因为x是余弦函数或正弦函数,为了便于计算,我们引入复数概念。欧拉公式是一个可以将代数与几何完美的联系起来的公式,它也使复杂的三角函数计算变为简单的指数计算。如式24
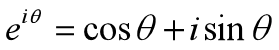
比如,当我们的力F是一个余弦波,且相位滞后为Δ,则力由余弦形式变为复数指数形式如式25
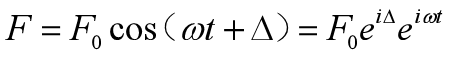
当然x也是复数,x微商如式26

所以,式23可以变为式27
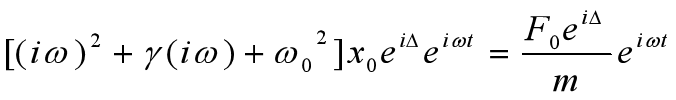
为了求解x,则式27可变形为式28

根据欧拉公式,式28中分母中的内容可写成式29

所以,式28可变为式30,
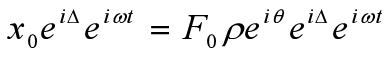
我们现在取式30的实数部分,则变为式31
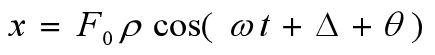
式31告诉我们,有阻尼的受迫振动的振幅是由F0和ρ共同决定。而共振,最主要关注的是振动的能量。根据式14,我们知道振动的能量与振幅的平方成正比。也就是说,振动的能量与模ρ的平方成正比,换句话说,模ρ的平方大小完全代表了能量大小。所以,求出模ρ的大小或模的平方大小是必不可少的内容。根据复数公式可知,模的平方等于共轭复数的积,所以可以得到式32
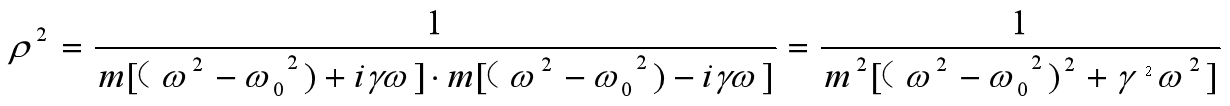
如果摩擦系数γ很小且ω接近ω0时,我们得到一个近似公式,虽然是近似公式,但非常有现实意义且非常正确了。因为我们主要关注的部分是共振部分。
所以,(ω0-ω)(ω0+ω)=2ω0(ω0-ω),γω=γω0,则式32变形为
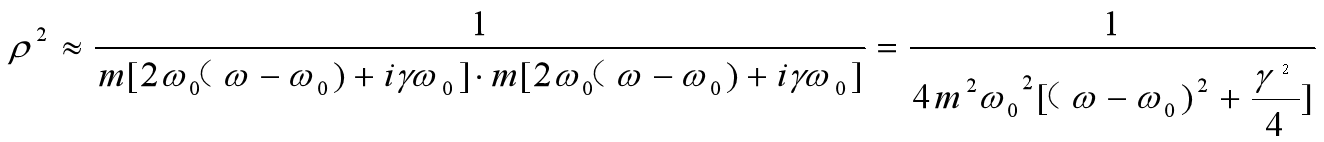
由于模的平方代表了能量,能量的一半也就意味着是模的平方值的一半。之所以要考虑能量的一半值,是因为共振是一种能量突然激发状态,讨论能量的一半非常现实意义。所以,通过式32求模ρ的平方的一半值后,我们发现可以得到一个非常神奇的结论:见式33(过程就不写了)
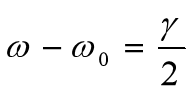
或者写成式34
![]()
相信大家看明白了,γ不仅仅是摩擦系数,当它足够小时,它还代表共振的频率宽度。换句话说,当摩擦的影响越小,共振越尖锐。共振能量与频率ω的关系图如下:
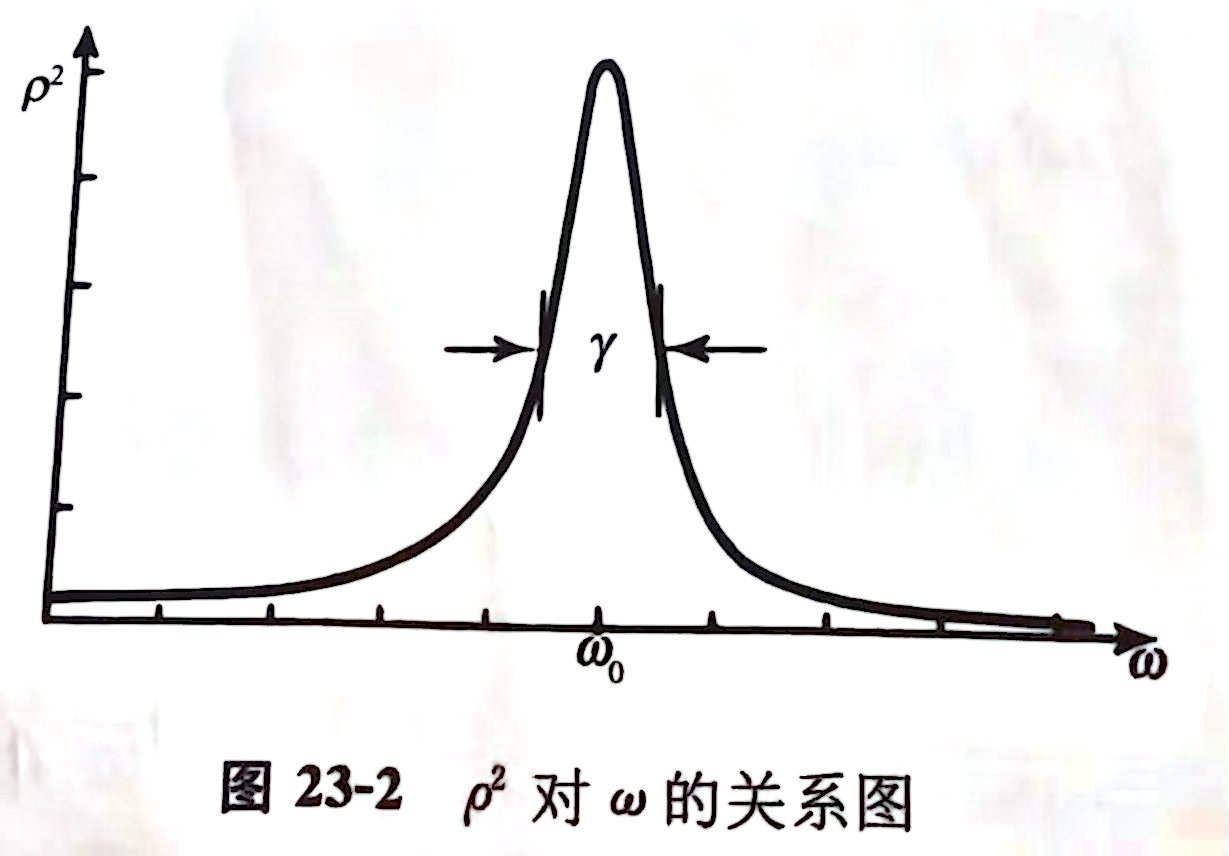
有人建议用式35来量度共振的宽度
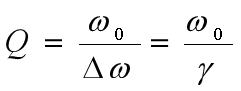
这个式子说明,共振越窄,Q值就越高。当Q为1000时,说明这个共振的宽度只有固有频率的千分之一。
同时,通过桥梁的固有频率和一半能量的频率可以求出桥梁结构的阻抗情况和共振宽度情况。(提一句,桥梁的共振频率一般在7.5Hz左右)。
Was this helpful?
0 / 0